С 19 векторы в пространстве. Векторы. Решить задачу на векторы самостоятельно, а затем посмотреть решение

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Определение 1

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .

Определение 2

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Определение 3

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектора A B → принято обозначать так A B → .

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин "длина вектора". Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Определение 4

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными .

Определение 5

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными .

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Определение 6

Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → b → .

Определение 7

Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↓ b → .

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Определение 8

Равными называются сонаправленные вектора, у которых длины равны.

Определение 9

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .

Определение 9

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Определение 10

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Определение

Скалярная величина - величина, которая может быть охарактеризована числом. Например, длина, площадь , масса, температура и т.д.

Вектором называется направленный отрезок $\overline{A B}$; точка $A$ - начало, точка $B$ - конец вектора (рис. 1).

Вектор обозначается либо двумя большими буквами - своим началом и концом: $\overline{A B}$ либо одной малой буквой: $\overline{a}$.

Определение

Если начало и конец вектора совпадают, то такой вектор называется нулевым . Чаще всего нулевой вектор обозначается как $\overline{0}$.

Векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).

Определение

Два коллинеарных вектора $\overline{a}$ и $\overline{b}$ называются сонаправленными , если их направления совпадают: $\overline{a} \uparrow \uparrow \overline{b}$ (рис. 3, а). Два коллинеарных вектора $\overline{a}$ и $\overline{b}$ называются противоположно направленными , если их направления противоположны: $\overline{a} \uparrow \downarrow \overline{b}$ (рис. 3, б).

Определение

Векторы называются компланарными , если они параллельны одной плоскости или лежат в одной плоскости (рис. 4).

Два вектора всегда компланарны.

Определение

Длиной (модулем) вектора $\overline{A B}$ называется расстояние между его началом и концом: $|\overline{A B}|$

Подробная теория про длину вектора по ссылке .

Длина нулевого вектора равна нулю.

Определение

Вектор, длина которого равна единице, называется единичным вектором или ортом .

Векторы называются равными , если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.

Все определения и теоремы, связанные с векторами на плоскости, верны и для пространства. Напомним основные определения.

Чтобы определить вектор нам понадобится

Определение

Направленным отрезком называется упорядоченная пара точек пространства. Направленные отрезки называются равными , если они имеют равную длину и направление.

Определение

Вектором называется множество всех равных между собой направленных отрезков.

Векторы обычно обозначают строчными латинскими буквами со стрелкой сверху: $\vec{a}$, $\vec{b}$, $\vec{c}$. Направленные отрезки обозначают, указывая начало и конец, также со стрелкой сверху: $\vec{AB}$.

Вектор - множество, состоящее из бесконечного числа элементов. Часто про направленный отрезок говорят "вектор". Если $\vec{AB} \in \vec{a}$, то говорят, что направленный отрезок $\vec{AB}$ изображает вектор $\vec{a}$. При этом на чертеже рисуется направленный отрезок, а говорят про него "вектор". Например, когда мы говорим "отложим вектор $\vec{r}$ от точки $O$, то имеется в виду, что мы строим направленный отрезок $\vec{OR}$, изображающий вектор $\vec{r}$.

Определение

Векторы называются равными , если равны изображающие их направленные отрезки.

Над векторами можно производить операции сложения и вычитания, а также умножать данный вектор на действительное число.

Из планиметрии известны правило треугольника: $\vec{a}+\vec{b} = \vec{c}$,

правило параллелограмма: $\vec{a}+\vec{b} = \vec{c}$

и правило ломаной сложения векторов для плоскости, которые верны и в пространстве.

Правило ломаной сложения векторов

Если $A_1, \, A_2, \, \dots, \, A_n$ - произвольные точки пространства, то

$ \vec{A_1A_2} + \dots + \vec{A_{n-1}A_n} = \vec{A_1A_n}. $

Кроме того, в пространстве справедливо

Правило параллелепипеда

Если $\vec{OA} \in \vec{a}$, $\vec{OB} \in \vec{b}$, $\vec{OC} \in \vec{c}$, то, построив на направленных отрезках параллелепипед $OAEBCFDG$, можно найти направленный отрезок $\vec{OD}$, изображающий вектор $\vec{d}$, который является суммой векторов $\vec{a}, \, \vec{b}, \, \vec{c}.$

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие вектора

Прежде чем Вы узнаете всё о векторах и операциях над ними, настройтесь на решение несложной задачи. Есть вектор Вашей предприимчивости и вектор Ваших инновационных способностей. Вектор предприимчивости ведёт Вас к Цели 1, а вектор инновационных способностей - к Цели 2. Правила игры таковы, что Вы не можете двигаться сразу по направлениям двух этих векторов и достигнуть сразу двух целей. Векторы взаимодействуют, или, если говорить математическим языком, над векторами производится некоторая операция. Результатом этой операции становится вектор "Результат", который приводит Вас к Цели 3.

А теперь скажите: результатом какой операции над векторами "Предприимчивость" и "Инновационные способности" является вектор "Результат"? Если не можете сказать сразу, не унывайте. По мере изучения этого урока Вы сможете ответить на этот вопрос.

Как мы уже увидели выше, вектор обязательно идёт от некоторой точки A по прямой к некоторой точке B . Следовательно, каждый вектор имеет не только числовое значение - длину, но также физическое и геометрическое - направленность. Из этого выводится первое, самое простое определение вектора. Итак, вектор - это направленный отрезок, идущий от точки A к точке B . Обозначается он так: .

А чтобы приступить к различным операциям с векторами , нам нужно познакомиться с ещё одним определением вектора.

Вектор - это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z ) . Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.

Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в конечной точке.

Все остальные термины - это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.

Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.

Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка . Это отрезок, у которого различают начало и конец.

Если A - начало вектора, а B - его конец, то вектор обозначается символом или одной строчной буквой . На рисунке конец вектора указывается стрелкой (рис. 1)

Длиной (или модулем ) геометрического вектора называется длина порождающего его отрезка

Два вектора называются равными , если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.

В физике часто рассматриваются закреплённые векторы , заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным . Мы договоримся рассматривать только свободные векторы .

Линейные операции над геометрическими векторами

Умножение вектора на число

Произведением вектора на число называется вектор, получающийся из вектора растяжением (при ) или сжатием (при ) в раз, причём направление вектора сохраняется, если , и меняется на противоположное, если . (Рис. 2)

Из определения следует, что векторы и = всегда расположены на одной или на параллельных прямых. Такие векторы называются коллинеарными . (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить "коллинеарны".) Справедливо и обратное утверждение: если векторы и коллинеарны, то они связаны отношением

Следовательно, равенство (1) выражает условие коллинеарности двух векторов.

Сложение и вычитание векторов

При сложении векторов нужно знать, что суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец - с концом вектора , при условии, что начало вектора приложено к концу вектора . (Рис. 3)

Это определение может быть распределено на любое конечное число векторов. Пусть в пространстве даны n свободных векторов . При сложении нескольких векторов за их сумму принимают замыкающий вектор, начало которого совпадает с началом первого вектора, а конец - с концом последнего вектора. То есть, если к концу вектора приложить начало вектора , а к концу вектора - начало вектора и т.д. и, наконец, к концу вектора - начало вектора , то суммой этих векторов служит замыкающий вектор , начало которого совпадает с началом первого вектора , а конец - с концом последнего вектора . (Рис. 4)

Слагаемые называются составляющими вектора , а сформулированное правило - правилом многоугольника . Этот многоугольник может и не быть плоским.

При умножении вектора на число -1 получается противоположный вектор . Векторы и имеют одинаковые длины и противоположные направления. Их сумма даёт нулевой вектор , длина которого равна нулю. Направление нулевого вектора не определено.

В векторной алгебре нет необходимости рассматривать отдельно операцию вычитания: вычесть из вектора вектор означает прибавить к вектору противоположный вектор , т.е.

Пример 1. Упростить выражение:

.

,

то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности, также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед вычислением произведений векторов.

Пример 2. Векторы и служат диагоналями параллелограмма ABCD (рис. 4а). Выразить через и векторы , , и , являющиеся сторонами этого параллелограмма.

Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам. Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Результат - требуемые в условии задачи векторы:

Есть все основания полагать, что теперь Вы правильно ответили на вопрос о векторах "Предприимчивость" и "Инновационные способности" в начале этого урока. Правильный ответ: над этими векторами производится операция сложения.

Решить задачи на векторы самостоятельно, а затем посмотреть решения

Как найти длину суммы векторов?

Эта задача занимает особое место в операциях с векторами, так как предполагает использование тригонометрических свойств. Допустим, Вам попалась задача вроде следующей:

Даны длины векторов и длина суммы этих векторов . Найти длину разности этих векторов .

Решения этой и других подобных задач и объяснения, как их решать - в уроке "Сложение векторов: длина суммы векторов и теорема косинусов ".

А проверить решение таких задач можно на Калькуляторе онлайн "Неизвестная сторона треугольника (сложение векторов и теорема косинусов)" .

А где произведения векторов?

Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки "Скалярное произведение векторов " и "Векторное и смешанное произведения векторов ".

Проекция вектора на ось

Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:

Как известно, проекцией точки A на прямую (плоскость) служит основание перпендикуляра , опущенного из этой точки на прямую (плоскость).

Пусть - произвольный вектор (Рис. 5), а и - проекции его начала (точки A ) и конца (точки B ) на ось l . (Для построения проекции точки A ) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.

Составляющей вектора на оси l называется такой вектор , лежащий на этой оси, начало которого совпадает с проекцией начала, а конец - с проекцией конца вектора .

Проекцией вектора на ось l называется число

,

равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l , и со знаком минус, если эти направления противоположны.

Основные свойства проекций вектора на ось:

1. Проекции равных векторов на одну и ту же ось равны между собой.

2. При умножении вектора на число его проекция умножается на это же число.

3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.

4. Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:

.

Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:

Находим окончательную проекцию суммы векторов:

Связь вектора с прямоугольной декартовой системой координат в пространстве

Знакомство с прямоугольной декартовой системой координат в пространстве состоялось в соответствующем уроке , желательно открыть его в новом окне.

В упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс , ось 0y – осью ординат , и ось 0z – осью аппликат .

С произвольной точкой М пространства свяжем вектор

называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:

Числа x, y, z называются координатами точки М , соответственно абсциссой , ординатой и аппликатой , и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).

Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором (или ортом ) оси. Обозначим через

Соответственно орты координатных осей Ox , Oy , Oz

Теорема. Всякий вектор может быть разложен по ортам координатных осей:

(2)

Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.

После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме

Представления вектора в виде (2) и (3) тождественны.

Условие коллинеарности векторов в координатах

Как мы уже отмечали, векторы называются коллинеарными, если они связаны отношением

Пусть даны векторы . Эти векторы коллинеарны, если координаты векторов связаны отношением

,

то есть, координаты векторов пропорциональны.

Пример 6. Даны векторы . Коллинеарны ли эти векторы?

Решение. Выясним соотношение координат данных векторов:

.

Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.

Длина вектора и направляющие косинусы

Вследствие взаимной перпендикулярности координатных осей длина вектора

равна длине диагонали прямоугольного параллелепипеда, построенного на векторах

и выражается равенством

(4)

Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.

Пусть в заданной системе координат начало вектора находится в точке

а конец – в точке

Из равенства

Следует, что

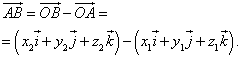
или в координатной форме

Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора . Формула (4) в этом случае примет вид

Направление вектора определяют направляющие косинусы . Это косинусы углов, которые вектор образует с осями Ox , Oy и Oz . Обозначим эти углы соответственно α , β и γ . Тогда косинусы этих углов можно найти по формулам

Направляющие косинусы вектора являются также координатами орта этого вектора и, таким образом, орт вектора

.

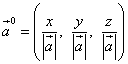
Учитывая, что длина орта вектора равна одной единице, то есть

,

получаем следующее равенство для направляющих косинусов:

Пример 7. Найти длину вектора x = (3; 0; 4).

Решение. Длина вектора равна

Пример 8. Даны точки:

Выяснить, равнобедренный ли треугольник, построенный на этих точках.

Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:

Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник является равнобедренным.

Пример 9. Найти длину вектора и его направляющие косинусы, если .

Решение. Координаты вектора даны:

.

Длина вектора равна квадратному корню из суммы квадратов координат вектора:

.

Находим направляющие косинусы:

Решить задачу на векторы самостоятельно, а затем посмотреть решение

Операции над векторами, заданными в координатной форме

Пусть даны два вектора и , заданные своими проекциями:

Укажем действия над этими векторами.

Лекция 3. Векторы. Системы линейных уравнений.

Векторы

Цель изучения темы состоит в обобщении понятия вектора, с которым студенты знакомы по школьной программе и расширение ее систематического кругозора.

Векторы на плоскости и в пространстве.

Вектор – это направленный отрезок . Точка А – начало вектора, точка В – конец вектора (рис. 3.1.1). Можно использовать обозначение .

Длиной (модулем) вектора называется число, равное длине вектора. Обозначается модуль вектора символом или . Если модуль вектора , вектор называется нулевым ; направление нулевого вектора произвольно.

Два вектора называются коллинеарными , если они параллельны одной прямой (или лежат на одной прямой), в этом случае пишут . Нулевой вектор коллинеарен любому вектору.

Два вектора равны , то есть , если выполняется три условия: ; и и одинаково направлены.

Произведением вектора ā на число (скаляр) λ называется вектор , удовлетворяющий следующим условиям: , векторы и сонаправлены, если и направлены в противоположные стороны, если . Если , вектор называется противоположным вектору .

Таким образом, условие является достаточным для коллинеарности вектором и ;

Сложение векторов. Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора при условии, что начало вектора совпадает с концом вектора (правило треугольника) (см. рис. 3.1.2).

Так как вектор , то для получения суммы двух векторов можно использовать правило параллелограмма : суммой двух векторов является вектор-диагональ параллелограмма, построенного на векторах и , выходящий их общего начала обоих векторов-слагаемых.

Сумма нескольких векторов находится по правилу многоугольника : чтобы найти сумму нескольких векторов , нужно последовательно совместить начало следующего вектора-слагаемого с концом предыдущего; тогда вектор, проведенный из начала первого вектора в конец последнего называется суммой всех данных векторов (рис. 3.1.3).

Разностью двух векторов называется сумма . Если вектор , то по аналогии с суммой двух векторов этот вектор является диагональю параллелепипеда, построенного на трех векторах как на сторонах (рис. 3.1.4).

Рассмотрим вектор в плоскости. Перенесем в начало координат системы хОу .

Получим вектор . Координатами вектора называются координаты точки М (х ;у ). Введем на осях координат векторы i и j – единичной длины (рис. 3.1.5).

Очевидно, или или . Если вектор рассматривается в трехмерном пространстве, где точка М характеризуется тремя координатами, то есть M (x,y,z ) , то вектор можно представить в виде:

xi yj zk , (3.1.1)

где i, j, k – единичные векторы, лежащие на осях координат. Пусть , . Найдем сумму и разность этих векторов:

Сложение векторов и умножение вектора на скаляр подчиняется следующим свойствам:

Доказательства вытекают на основании (3.1.2).

Определение. Скалярным произведением векторов и называется число равно произведению модулей этих векторов на косинус угла φ между ними, то есть . (3.1.3)

Из (3.1.3) вытекают свойства скалярного произведения:

4) если , то .

Используя свойства скалярного произведения, можно найти скалярное произведение двух векторов в координатной форме. Если , , то ; если - условие перпендикулярности векторов.

Если векторы коллинеарны, то есть , то - условие коллинеарности векторов.

Понятие n -мерного вектора. Векторное пространство. Линейная комбинация и линейная зависимость векторов.

Понятие вектора можно обобщить.

Определение. n -мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х 1 , х 2 ,…, х n) , х i – компоненты вектора Х .

Понятие n -мерного вектора широко используется в экономике. Например, некоторый набор товаров можно охарактеризовать вектором , а соответствующие цены – вектором .

Два n -мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты: , .

По аналогии с геометрическими векторами вводятся: сумма векторов с компонентами , ; разность векторов с компонентами , , с теми же свойствами.

Скалярное произведение n -мерных векторов:

Если X - набор товаров, а Y - соответствует ценам за единицу каждого товара, то стоимость всем товаров:

Определение. Множество векторов с действительными компонентами, в котором определены операции сложения (вычитания) и умножения вектора на скаляр, удовлетворяющего приведенным выше свойствам называется векторным пространством.

Определение. Вектор называется линейной комбинацией векторов векторного пространства, если

, (3.1.4)

где - любые действительные числа.

Определение. Векторы называются линейно зависимыми, если существуют такие числа , не равные одновременно нулю, что линейная комбинация .

В противном случае векторы () называются линейно независимыми.

Если векторы линейно зависимы, то хотя бы один из них линейно выражается через остальные. Покажем это. Пусть векторы () линейно зависимы, то естьn), следовательно

Решив систему любым методом (например, методом Крамера), получим ее решение: , , . Разложение вектора по базису имеет вид .